104. The Representation of Sound (2)
- Hui Wang

- Dec 1, 2023
- 8 min read
Updated: Jan 19, 2024
In our previous exploration titled 'The Representation of Sound (1)', we ignited a spark of thought: What happens behind the scenes when the 'sound' our ears hear transforms into 'audio data' processed by our phones and computers? Based on this question, we have already delved into two fascinating topics: 'What is the definition of sound?' and 'What are the characteristics of sound?'. Now, we will continue this journey and delve into the next intriguing puzzle: 'How can we describe sound using the language of mathematics'.
How can we paint the contours of sound with the brush of mathematics?
Once we have a clear understanding of the definition of sound and have identified its characteristics, we can then step into a new realm: crafting precise maps of these features using the language of mathematics.
The Mathematical Description of Loudness
Loudness is a subjective psychological measure reflecting the strength of sound as perceived by the human ear, allowing us to arrange sounds in a sequence from quiet to loud.
Correspondingly, the objective physical quantities related to the strength of sound include 'sound intensity' and 'sound pressure'. To understand sound intensity, we first need to grasp the concept of 'sound energy'.
Sound energy is the energy imparted to the medium when sound propagates through it. Since sound waves originate from the vibration of particles deviating from their equilibrium position, sound energy is defined as the sum of the kinetic energy of particle vibration and the potential energy of particles deviating from their equilibrium position, measured in 'Joules (J)'.
Sound intensity is the average sound energy passing through a unit area perpendicular to the direction of sound propagation per unit time, represented by I. Its unit is 'Watts per square meter (W/m²)'. The range of sound intensity perceivable by the human ear is vast (0.000000000001~1 W/m²). Moreover, psychophysical research shows that our perception of the strength of sound is not directly proportional to sound intensity but to its logarithm. Therefore, we use 'Sound Intensity Level' to represent sound intensity.
Though theoretically sound intensity can objectively measure the amplitude of sound waves at a point, it is not a commonly used measure in everyday work. Since the human ear is sensitive to pressure changes and pressure measurements are relatively easy to perform, sound pressure is more commonly used to represent the amplitude of sound waves.
Sound pressure refers to the change in pressure caused by the vibration of a sound wave passing through a medium, measured in 'Newtons per square meter (N/m²)' or 'Pascals (Pa)', and represented by P. When sound propagates through air, the vibration of objects causes the surrounding air to vibrate, forming waves of alternating high and low pressure. The root mean square value of sound pressure, known as effective sound pressure, is typically used. Unless specified, the term 'sound pressure' usually refers to effective sound pressure. Like sound intensity, the range of sound pressure is vast (0.00002~20 N/m²), and our perception of the strength of sound is proportional to the logarithm of sound pressure, hence we use 'Sound Pressure Level' to represent it.
The relationship between sound pressure and sound intensity
In a free sound field, the sound intensity at a point is directly proportional to the square of the sound pressure at that point and inversely proportional to the product of the medium's density and the speed of sound.

P, represents effective sound pressure (N/m²)
q, represents medium density (kg/m³)
c, represents the speed of sound in the medium (m/s)
qc, represents the characteristic impedance of the medium, which is 415N·s/m³ in 20℃ air
The term 'level' is used for relative comparisons and is dimensionless, such as Sound Intensity Level and Sound Pressure Level.
Sound Intensity Level (SIL), with 10-12 W/m² as the reference value, is calculated as the logarithm of the ratio of any sound intensity to this reference value, multiplied by 10, and measured in 'decibels (dB)'. Why multiply by 10? This comes from the definition of the units 'Bel' and 'Decibel'. The Bel unit is large, so its tenth part, the 'Decibel', is used to amplify the calculated values and highlight differences.

Li, represents Sound Intensity Level (dB)
I, represents sound intensity (W/m²)
I0, represents the constant of the reference sound intensity, valued at 10-12 W/m²
Sound Pressure Level (SPL), with 2×10-5 N/m² as the reference value, is calculated as the logarithm of the ratio of any sound pressure to this reference value, multiplied by 20, and is also measured in 'decibels (dB)'. Why 20? By incorporating the relationship between sound pressure and sound intensity into the formula for calculating Sound Intensity Level, the formula for Sound Pressure Level can be derived.

Lp, represents Sound Pressure Level (dB)
P, represents sound pressure (N/m² or Pa)
P0, represents the constant of the reference sound pressure, valued at 2×10-5 Pa
The human ear's perception of sound is related to sound pressure, but not solely. It also depends on frequency. Sounds at the same Sound Pressure Level but different frequencies can be perceived as having different loudness.
To quantitatively estimate the loudness of a pure tone, it can be compared in loudness to a pure tone of 1000 Hz at a certain Sound Pressure Level. When these two sounds are perceived as having the same loudness, the Sound Pressure Level of the 1000 Hz pure tone is defined as the Loudness Level of the pure tone at that frequency. The unit for Loudness Level is 'Phon'.
For example, for a pure tone of 1000 Hz frequency to reach a loudness of 40 Phons, according to the equal-loudness contour graph, its Sound Pressure Level needs to be 40 dB SPL.
The following chart, with frequency on the horizontal axis and Sound Pressure Level on the vertical axis, shows the undulating lines of the equal-loudness contours. These lines represent the relationship between the frequency of sound and Sound Pressure Level at the same Loudness Level.

Loudness level not only captures the physical effects of sound but also considers the auditory physiological effects of the human ear, representing our subjective evaluation of sound.
In our daily conversations, when we talk about decibels, we are actually referring to the sound pressure level. For instance:
1 decibel - A sound just audible to our hearing.
Below 15 decibels - Feels quiet, like a soft whisper.
30 decibels - The volume of a whisper.
40 decibels - The humming noise of a refrigerator.
60 decibels - The volume of normal conversation.
70 decibels - Like walking in a bustling city area.
85 decibels - The sound of cars moving on the road.
95 decibels - The roar of a starting motorcycle.
100 decibels - The noise of a construction drill.
110 decibels - The loudness of karaoke.
120 decibels - The roar of an airplane taking off.
150 decibels - The sound of fireworks and firecrackers.
As the list shows, the sound of an airplane taking off is 120 decibels. If we know the frequency of this sound, we can accurately determine its loudness level.
The Mathematical Expression of Pitch
Pitch is the subjective perception of the highness or lowness of a sound by the human ear. The objective measure corresponding to pitch is the 'frequency' of the sound wave. The highness or lowness of pitch is determined by the vibration frequency, with a direct positive correlation between the two.
We are relatively familiar with measuring frequency, which is expressed in 'Hertz (Hz)'. But how do we measure pitch? One method is to use 'mel' as the unit of pitch. A pure tone with a frequency of 1000 Hz and a sound pressure level of 40 dB is defined as 1000 mel. Based on this standard, other pure tones that sound twice as high are termed 2000 mel, and those that sound half as high are 500 mel. In this way, we can establish a complete scale of pitch within the entire audible frequency range.
The pitch of musical tones (complex tones) is more complicated, generally considered to be determined mainly by the frequency of the fundamental tone.
The relationship between pitch and frequency is illustrated in the following chart:

Below 500 Hertz, the relationship between pitch and frequency is almost linear, but it becomes logarithmic for mid to high frequencies.
Pitch is usually quantified using 'scientific pitch notation' or a combination of letters and numbers that represent the fundamental frequency.
If the frequency of two notes differs by an integer multiple, they sound very similar. Thus, we place these notes in the same 'pitch set'. If the frequency difference between two notes is a multiple of two, we say they are an octave apart. To fully describe a note, we must specify both its category and the octave it belongs to. In traditional music theory, we use the first seven Latin letters: A, B, C, D, E, F, G (ascending in pitch in this order) along with some variations (as detailed below) to denote different notes. These letter names repeat, with G followed by a higher octave A. To indicate notes of the same name but different heights, scientific pitch notation uses letters and Arabic numerals to clearly mark the note's position. For example, the standard tuning pitch of 440 Hertz is named A4, with the next higher octave being A5, and so on; below A4 are A3, A2, etc. Traditionally, due to historical reasons, octave numbering starts with the C note and ends with B: C, D, E, F, G, A, B, ascending in pitch.
Sometimes, we add accidentals like sharps (♯) and flats (♭) next to the note names. These symbols indicate raising or lowering the original note by a semitone. In the twelve-tone equal temperament, the most widely used tuning system today, this means multiplying or dividing the original frequency by 2(1/12)=1.0594. So, raising a note by n semitones multiplies the frequency by 2(n/12), and lowering it by n semitones multiplies it by 2(-n/12). A sharp symbol (♯) means raising the note, and a flat symbol (♭) means lowering it, usually written after the note name, like F♯ for raised F, and B♭ for lowered B. Other accidental symbols like double sharps or double flats (raising or lowering a note by a whole tone or two semitones) are also used in traditional music theory. In cases of enharmonicity, we can use accidentals to denote the same pitch with different note names. For instance, raising B by a semitone to B♯ is actually the same pitch as C. However, removing these enharmonic equivalents, the complete chromatic scale adds five pitch sets to the original seven notes, with each adjacent pitch set being a semitone apart.
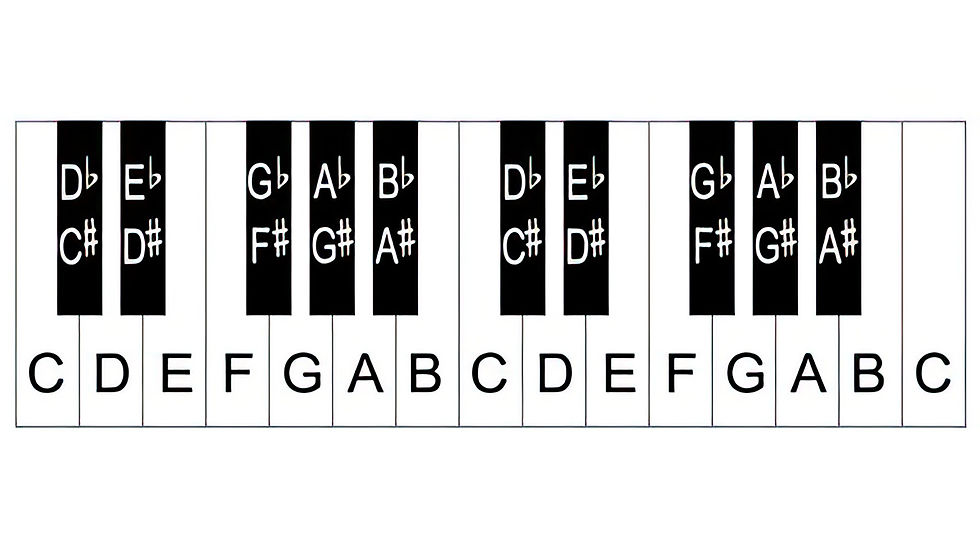
In the grand palace of music exploration, we notice that within the realm of seven whole tones, there lies a secret of only five semitones. Notably, between E and F, and between B and C, there are no semitones. To explain in detail, an octave actually consists of twelve semitones. Among these, seven (CDEFGAB) are called natural notes, and the other five are referred to as accidental notes. Usually, there is a gap of two semitones (a whole tone) between natural notes, but there are exceptions, like between E and F, and B and C, where there is only a gap of one semitone.
The chart below comprehensively shows the chromatic scale of semitones starting from middle C (C4) and spanning an upward octave:

Below is a comparison of some common notations and frequencies used in international music notation, as well as for tenor and soprano vocal ranges.

The Mathematical Interpretation of Timbre
In the world of sound, loudness can be thought of as describing the 'size' of a sound, and pitch depicts its frequency, both of which are relatively easy to understand.
But how do we understand the 'timbre' of a sound?
In reality, most sound waves are not simple sine waves but complex ones. These complex waveforms can be decomposed into a series of sine waves. Among these sine waves, there is a fundamental frequency, f0, representing the basic tone of the sound, and its harmonics, f1, f2, f3, f4, etc., which are integer multiples of f0 and correspond to the overtones of the sound. These harmonics have specific amplitude ratios. It's this unique ratio that gives each sound its characteristic quality, which we call timbre. Without harmonics, a pure fundamental frequency sine signal lacks musicality. Thus, the frequency range of musical sounds from instruments includes both the fundamental frequency and its harmonics.

The highness or lowness of a sound's pitch, as mentioned earlier, is determined by the fundamental frequency of the base tone. This is why different people singing the same pitch can sound so different: they share the same fundamental frequency, but their harmonics are completely different.
Therefore, the timbre of a sound is determined by its harmonic spectrum, or in other words, it is defined by the shape of the sound wave.
Follow me on:



Comments